作者:Nadav Kohen
点支付合约系列
Payment Points Part 1: Replacing HTLCsPayment Points Part 2: “Stuckless” Payments
Payment Points Part 3: Escrow Contracts
Payment Points Part 4: Selling Signatures
在闪电网络 v1.0 中,路由交易是由哈希时间锁合约(Hashed Timelock Contracts,HTLC)来实现的。这种合约的含义是有条件支付:如果 Bob 能揭示某个哈希值的原像,Alice 就会给他支付一笔比特币。否则,Alice 会在一段时间后拿回自己的比特币。
多个这样的合约可以用同一个 “支付哈希值” 串联起来。我们之前已经介绍过这种模式了,但现在不妨回顾一下:
假设 Alice 希望通过 Bob 给 Carol 支付 1 btc。那么 Alice 可以给 Bob 一个价值 1.01 的 HTLC 输出,条件是 Bob 必须提供对应于某个哈希值 H 的原像。而 Carol 是知道这个原像的。因此,Bob 找到 Carol,给她一个价值 1 btc 的 HTLC 输出,来交换对应于哈希值 H 的原像。Carol 通过向 Bob 公开这个原像获得了 1btc,然后 Bob 就拿着这个原像,从 Alice 处获得 1.01 btc。
HTLC 能够工作,也成功让闪电网络的路由支付变成原子化的(要么一条路径上的所有支付都成功,要么全都失败)。但使用支付哈希值来实现这一功能也带来了一些缺点。首先,给定的一条路径上的所有支付交易,都可以用同一个哈希值联系起来!这意味着两个共享信息的节点(比如,它们都是由同一个人运营的)就可以根据自己所收到的 HTLC 的哈希值、知道他们是不是在同一个支付路径上。这不仅让他们知道了我们不希望他们掌握的(关于路由的)信息,还让他们可以执行 “虫洞攻击” —— 他们可以串谋窃取两人之间的所有中间人的手续费 [1]。
假设 Mallory 和 Mike 是恶意的,并且发现了他们在同一条支付路径上。进一步地,假设 Mallory 收到了一个价值 1.1 btc 的 HTLC,而 Mike 收到了价值 1 btc、使用同一个哈希值的 HTLC。(这 0.1 btc 的差值来源于 Mallory 和 Mike 之间的中间人收取的手续费总和。) 如果 Mike 转发了交易、最终用 1 btc 换得了相关哈希值的原像,他可以直接把这个原像交给 Mallory,Mallory 可以(跟上家)拿到 1.1 btc —— 无需支付任何东西!Mallory 向自己的上家公开这个原像之后,路由会如常继续,这个路径上 Mallory 之前和 Mike 之后的节点,都对发生了什么一无所知。与此同时,Mallory 和 Mike 两人一共支出了 1 btc,获得了 1.1 btc,等于是拿走了两人之间的所有中间人原本可以获得的手续费。最糟糕的是,这些中间人的资金还锁在用不了的 HTLC 里,要等超时之后才能取回(因为 Mike 是个坏蛋,不会给他们任何提醒的);这些中间节点无法区分支付受阻到底是因为形势使然,还是恶意攻击!

有一个出色的提案可以解决这个问题(同时引入许多很酷的新特性),那就是把原像和哈希值换成 “标量(scalar)” 和 “点(point)”。也就是说,与其使用原像 a 和哈希值 h(a) 来使支付原子化,我们把 a 视作一个私钥并创建一个合约,要求合约的受益人必须揭示对应于某个公钥 A = a * G 的私钥,才可获得资金(此处的 G 是椭圆曲线上的一个点,因此 a * G = G + G + ... + G(即 G 相加 a 次)不会暴露有关这个私钥 a 的信息)。
到目前为止,我们还不确定能够解决问题,但是,从哈希函数转向(同态的)单向函数,意味着我们可以在公开的输出点上做运算(加法和乘法),这些运算就能反映出输入标量的特性而无需实际公开输入,比如 (a * G) + (b * G) = (a + b) * G(相比之下,hash(a) + hash(b) 可是跟 hash(a+b) 没有任何关系)。本质上,此处使用哈希锁的问题在于哈希运算会破坏信息,而在同态的单向函数中,信息不会被破坏。现在,我们使用这个好处把支付交易串联起来。
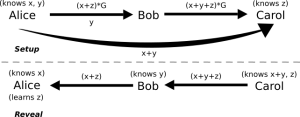
举例:Alice 希望通过 Bob 给 Carol 支付。
- Carol 生成一个秘密值 z,并(通过 invoice)把
z * G交给 Alice(译者注:invoice 是一段功能类似于收款码的信息) - Alice 现在选出两个随机数 x 和 y
- Alice 给 Bob 一个类似于 HTLC 的合约,只有 Bob 能够揭示一个与
(x + z) * G关联的私钥,也就是 (x + z),才能获得这些资金 - Alice 把 y 交给 Bob,并告诉他:Carol 知道
(x + z) * G + y * G的原像,也就是 (x + y + z),得到了这个值,减去自己提供的 y,就是 (x + z) - Alice 把 (x + y) 交给 Carol,这样不会暴露 x 和 y 中的任何一个
- Bob 也给 Carol 一个类似于 HTLC 的合约,只有 Carl 能够揭示
(x + y + z) * G所对应的私钥,也即 (x + y + z),才能获得资金 - Carl 向 Bob 揭示 (x + y) + z,获得合约中的资金
- Bob 计算出 (x + z),向 Alice 揭示,获得自己的资金
- Alice 检验 (x + z) - x = z,作为她的支付证明(这个支付证明甚至比我们当前的 哈希-原像 方案还要好,因为只有 Alice 知道了 z,而 Bob 并没有)
这个方案可以推广到使用任意数量的中间人的情形,只需为每个中间人增加一个随机数即可。因为每个中间人都使用完全不同的条件(随机数是一个一个加进去的),所以我们隐去了支付交易的关联!更美妙的是,Poelstra 已经证明,这个方案只需使用简单的 Schnorr 聚合签名即可实现,办法是使用 partial and adaptor 签名 [2] (Taproot 可以用于时间锁),所以闪电网络通道可以由小而简单的输出组成,在单方面关闭通道时提高隐私性并降低手续费 [3]。
想要 Schnorr 签名、partial and adaptor 签名以及它们如何实现点时间锁方案的详细解释,请看 Rene Pickhardt 的视频系列。
使用点和标量,我们可以隐去支付交易间的关联,同时保证路由支付的原子性。但这个方案有没有给我们带来别的一些功能呢?我最喜欢的三个用途是:重发 “受阻” 的支付,在闪电通道中启用第三方托管合约(escrow contract),以及启用免信任的签名销售。
我们会在后续文章中讨论这些依赖于点时间锁合约的新特性。